AOCL-BLAS: Boosting GEMM Performance for Small Matrices
Aug 12, 2025

Engineering GEMM Efficiency Beyond the Hot Path
In performance engineering, optimizations often focus on large, square matrices and high-throughput paths. However, real-world workloads—such as batched general matrix multiply (GEMMs), AI inference, and scientific simulations—frequently involve small or skinny matrices. Despite their size, these matrices occur so often that they can dominate the overall runtime. This blog focuses on refining AMD Optimizing CPU Libraries – Basic Linear Algebra Subprograms (AOCL-BLAS) GEMM kernels to handle these cases efficiently, leveraging architectural insights from AMD “Zen 4” and “Zen 5” architecture.
At the heart of most high-performance GEMM implementation lies the 5-loop algorithm, a hierarchical structure that decomposes matrix multiplication into nested loops for blocking, packing, and micro-kernel execution. This design is highly effective for large, square matrices, where cache reuse and computing throughput can be fully exploited.
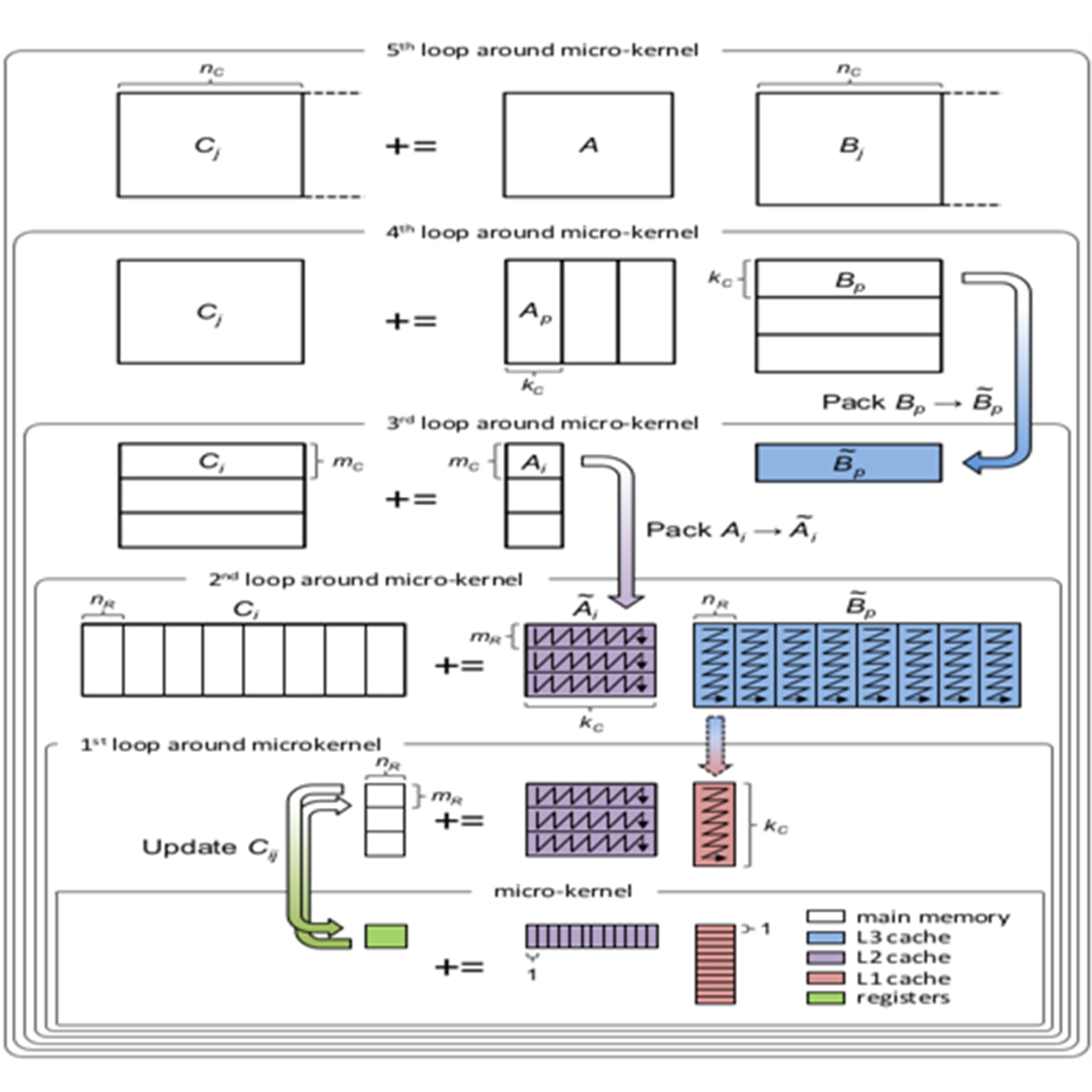
Figure 1: GotoBLAS Algorithm for Optimizing GEMM Operation
GotoBLAS algorithm for GEMM: This figure above presents the GotoBLAS algorithm for optimizing GEMM operation. It features a hierarchy of five nested loops surrounding a micro-kernel.
However, this same structure becomes a hidden cost when applied to skinny matrices that are too narrow, short, or simply too small. In these cases, the overhead of packing and blocking can outweigh the benefits, leading to suboptimal performance.
This blog is a story of refinement and precision — how we tuned AOCL-BLAS GEMM kernels for AMD Zen 4 and Zen 5 architecture, not by brute force, but by understanding the architecture, embracing the edge cases, and crafting solutions that shine even in the smallest corners of computation.
System Configuration
All performance measurements presented in this blog were conducted on the following system:
Processor: AMD EPYC™ 9755, 128-Core Processor (2 sockets, 256 cores total)
Base/Boost Frequency: 1.5 GHz (min) – 4.12 GHz (max)
Cache:
L1d: 12 MiB (256 × 48 KiB)
L1i: 8 MiB (256 × 32 KiB)
L2: 256 MiB (256 × 1 MiB)
L3: 1 GiB (32 × 32 MiB)
NUMA Nodes: 8
Memory: DDR5, 5600 MT/s, Total Size: 1.48 TB
Operating System: Red Hat Enterprise Linux 9.3
This configuration was consistently used across all benchmarks and performance charts in the blog.
Repeated Kernel Call & µOp Cache Inefficiency
In earlier implementations of the GEMM kernel within AOCL-BLAS, each micro-tile of the matrix was processed through an invocation of the gemm_kernel function. This was typically done inside the second loop of the 5-loop GEMM algorithm, which iterates over the M dimension. For every iteration, the offsets are recalculated, and a function is invoked to handle the current tile.
// gemm_kernel code block
// Loop 2 of the 5-loop GEMM algorithm
// This loop advances in steps of the micro-kernel block size (e.g., 24 for M dimension)
for (int i = 0; i < M; i += MR) // MR = micro-kernel block size for M (e.g., 24)
{
// Compute offsets for A and C based on current block row
int A_offset = i * lda; // lda = leading dimension of A
int C_offset = i * ldc; // ldc = leading dimension of C
// Call the micro-kernel on the current block
gemm_kernel(A_base_ptr + A_offset,
B_base_ptr,
C_base_ptr + C_offset,
...); // Additional parameters as needed
While this approach is functionally correct, it introduces significant performance penalties. This implementation causes fragmentation of the instruction stream, which increases the pressure on the 32KB instruction cache. This cache struggles to retain both the loop control logic and the relatively large body of the gemm_kernel() function.
Moreover, µOp cache and loop stream detector (LSD) in the “Zen” architecture, both critical for efficient frontend throughput, are optimized for tight, predictable instruction sequences. Frequent function calls disrupt this predictability, leading to µOp cache fragmentation and reduced LSD engagement. As a result, the frontend pipeline experiences stalls, and the overall throughput of GEMM operation degrades.
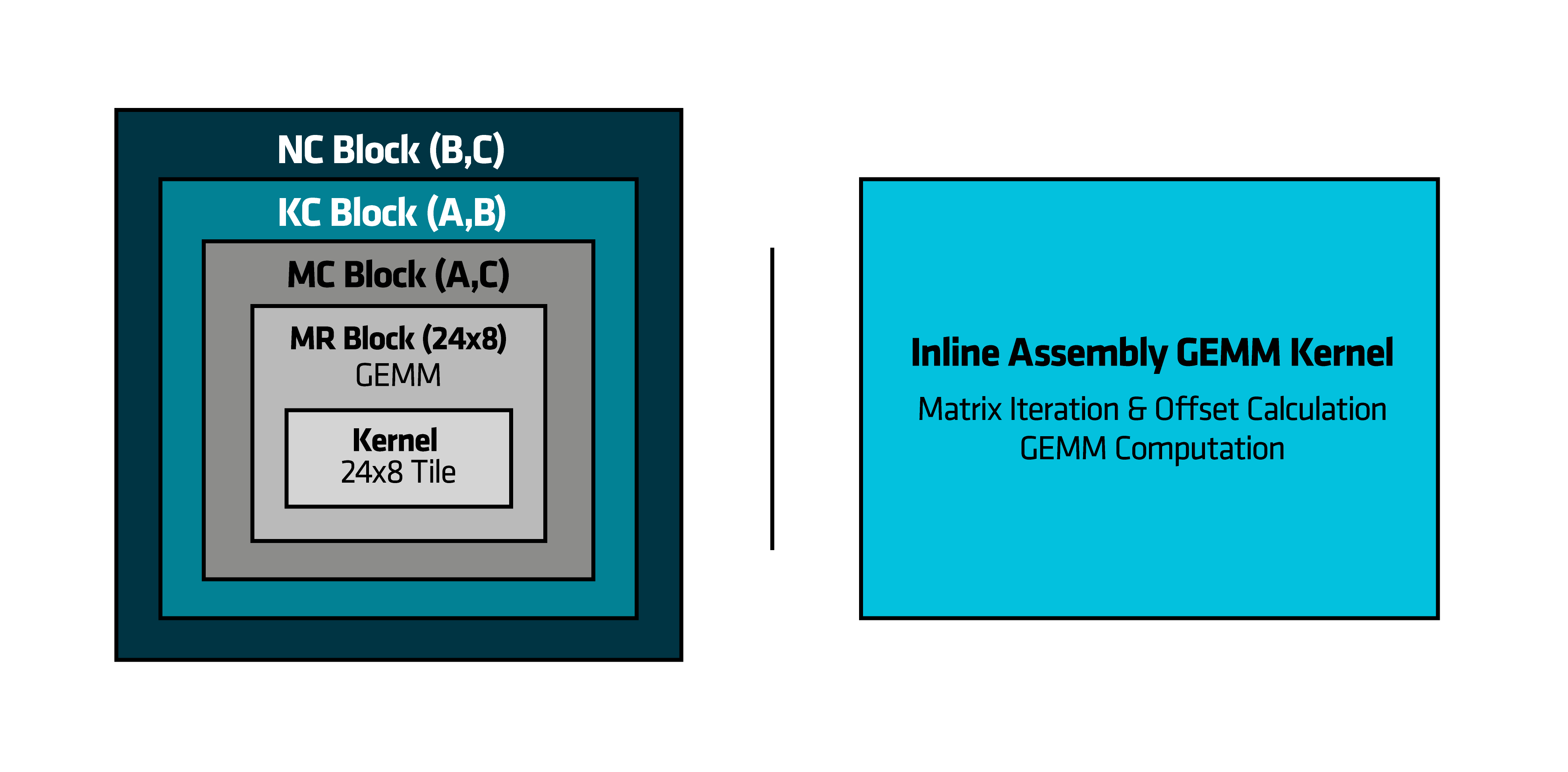
Figure 2: Visual Comparison of DGEMM Kernel Strategies: Baseline vs Optimized Execution
Hierarchical Blocking and nested loops surrounding the 24x8 micro-kernel vs Inline assembly kernel: The left side of the image shows a blocking and nested loops, while the right side highlights the inline assembly kernel, which implements the M loop directly within the kernel.
To address this, we restructured the kernel by pulling the micro-tile loop directly into the kernel function body using inline assembly. This change eliminated the need for repeated function calls, allowing the entire loop to execute as a contiguous block of instructions.
void gemm_kernel_with_internal_loop(...) {
begin_asm;
// Register-based loop
// Compute offsets, load, FMA, store, loop
end_asm;
}
The benefits were immediate: contiguous instruction stream improved I-cache locality, better µOp cache utilization, and consistent engagement of the LSD. This change significantly reduced the function call overhead, enabling faster front-end throughput.
The performance chart compares the baseline implementation with the optimized Double-precision General Matrix Multiply (DGEMM) kernel, showing 5% performance improvement. This improvement stems from reducing function call overhead and ensuring a more contiguous instruction stream.
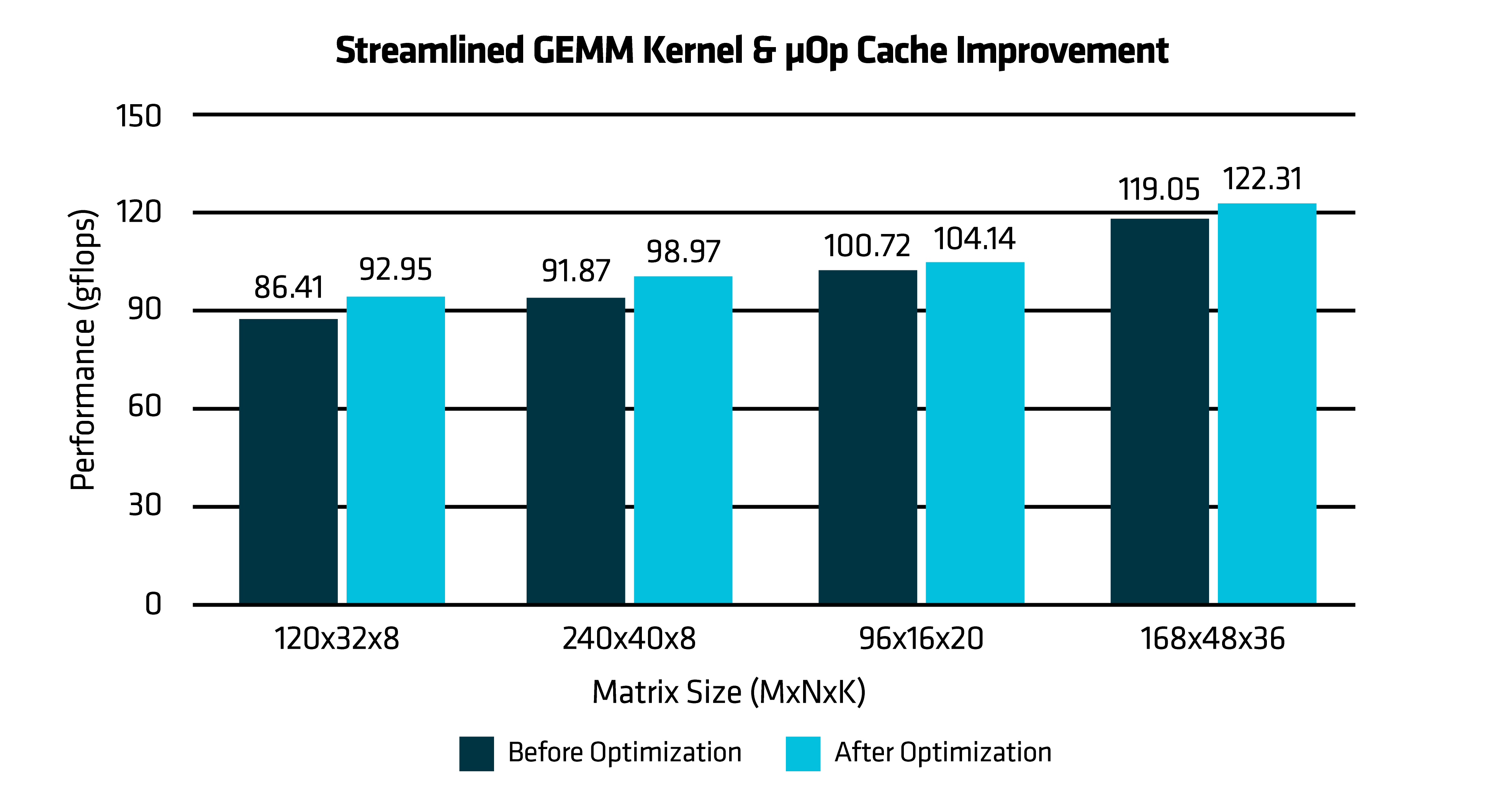
Figure 3: Streamlined GEMM Kernel & uop Cache Improvement
Performance gain from streamlined GEMM kernel & µOp Cache Improvements: The performance chart compares the baseline implementation with the optimized DGEMM kernel, showing 5% performance improvement. This improvement stems from reducing function call overhead and ensuring a more contiguous instruction stream. The x-axis lists various matrix sizes (MxNxK), while the y-axis shows the performance in gigaflops (GFLOPS).
Breaking Fused Multiply-Add (FMA) Dependency Chains
In high-performance GEMM kernels, fused multiply-add (FMA) instructions are the core computational workhorse. However, when multiple FMAs are issued back-to-back using the same destination register, they form a dependency chain. Each instruction must wait for the previous one to complete before it can execute, creating a bottleneck in the out-of-order execution engine. This pattern stalls the instruction scheduler and limits the number of operations that can be issued per cycle. On AMD “Zen 4” and “Zen 5” architecture, which are designed to exploit instruction-level parallelism, such dependency chains underutilize the available execution resources.
vfmadd231pd zmm0, zmm2, zmm30 // i.e. zmm0 = (zmm2 * zmm30) + zmm0 vfmadd231pd zmm0, zmm3, zmm31 // i.e. zmm0 = (zmm3 * zmm31) + zmm0 ⚠️stall
vfmadd231pd zmm0, zmm4, zmm30
vfmadd231pd zmm0, zmm5, zmm31
To eliminate this bottleneck, we restructured the FMA sequence by distributing the operations across multiple independent registers. Each FMA now writes to a separate accumulator, allowing the CPU to execute them in parallel. Once the independent FMAs are complete, their results are combined using a series of vaddpd instructions to produce the final output.
vfmadd231pd zmm10,zmm2, zmm30 // i.e. zmm10 = (zmm2 * zmm30) + zmm10
vfmadd231pd zmm11,zmm3, zmm31 // i.e. zmm11 = (zmm2 * zmm30) + zmm11
vfmadd231pd zmm15,zmm4, zmm30
vfmadd231pd zmm16,zmm5, zmm31
vaddpd zmm10, zmm11, zmm10 // i.e. zmm10 = zmm11 + zmm10
vaddpd zmm15, zmm16, zmm15
vaddpd zmm10, zmm15, zmm10
This approach breaks the dependency chain and frees the scheduler from issuing multiple FMAs simultaneously. The result is a smoother instruction flow, reduced stalls, and significantly higher throughput—especially in compute-bound inner loops where every cycle counts.
The performance chart compares the baseline implementation with the optimized DGEMM kernel, revealing an approximate 20% performance gain. This improvement is primarily attributed to breaking FMA dependency chains, enabling better instruction-level parallelism and improved CPU pipeline utilization.
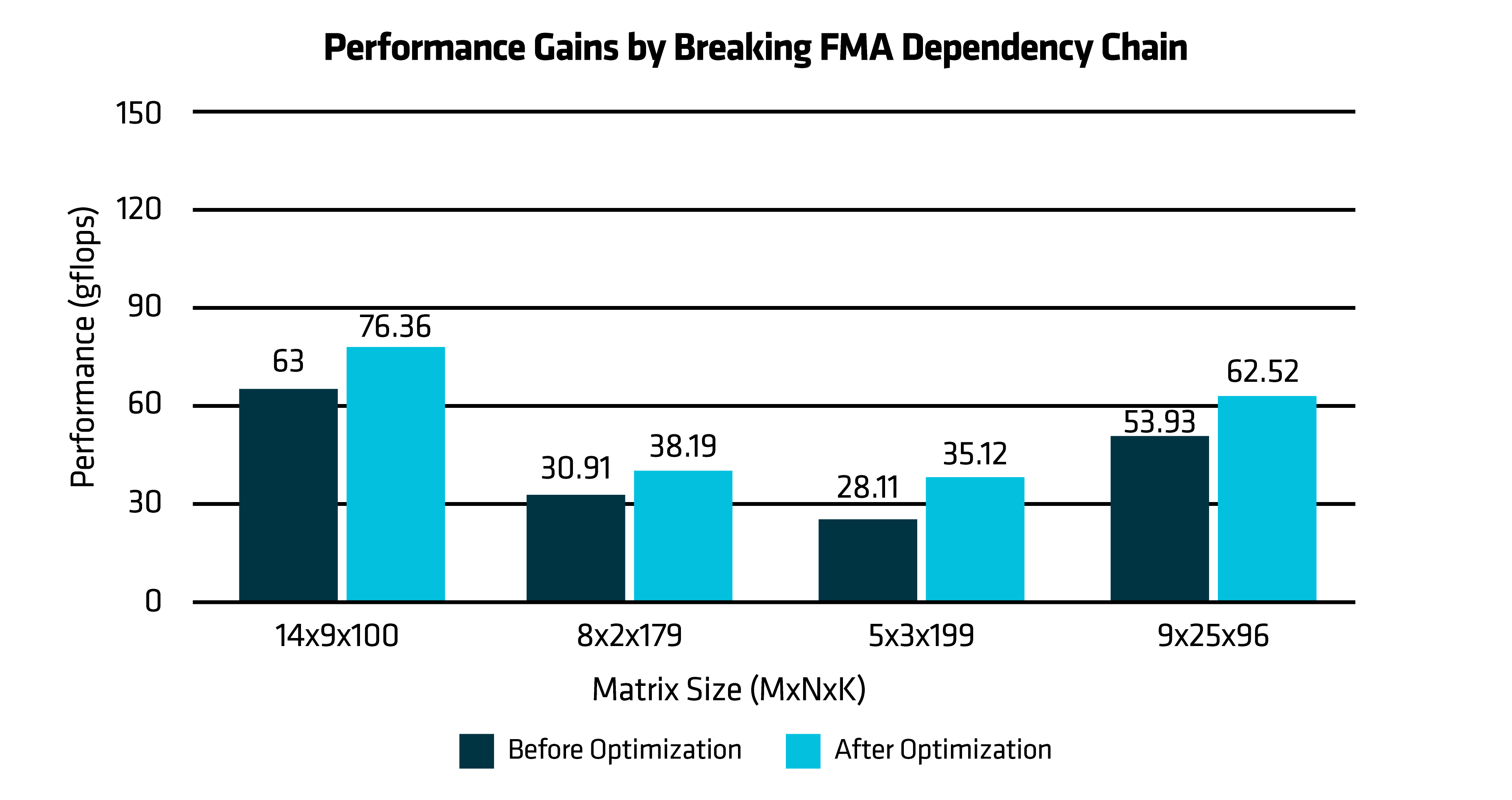
Figure 4: Performance Gains by Breaking FMA Dependency Chain
Performance Gains from Breaking FMA dependency chain in GEMM Kernel: The performance chart compares the baseline implementation with the optimized DGEMM kernel, revealing an approximate 20% performance gain. This improvement is primarily attributed to breaking FMA dependency chains, enabling better instruction-level parallelism and improved CPU pipeline utilization.
Fused Loads + FMAs: Reducing Instruction & µOps Count
In baseline GEMM kernel implementations, scalar values are often loaded from memory, broadcast across a vector register, and then used in an FMA operation. This three-step sequence —load, broadcast, and compute— introduces unnecessary instruction overhead and increases register pressure.
//Load 64-bit scalar from memory at [rbx] and broadcast to all 8 lanes of zmm0
vbroadcastsd zmm0,mem(rbx)
vfmadd231pd zmm6,zmm0, zmm1 // i.e. zmm6 = (zmm0 * zmm1) + zmm6
This pattern not only inflates the instruction count but also introduces additional dependencies between operations. Each step must be completed before the next can begin, limiting instruction-level parallelism and increasing decode pressure on the front-end pipeline.
Modern AMD “Zen” microarchitectures, starting with “Zen 4”, support AVX-512 instructions that allow memory operands to be directly fused into FMA operations. By leveraging this capability, we replaced the traditional three-instruction sequence with a single vfmadd231pd that performs the load, broadcast, and computation in one step:
vfmadd231pd zmm6, zmm1, qword ptr [rbx]{1to8} // i.e. zmm6 = (zmm1 * broadcast([rbx])) + zmm6
This fused instruction reduces the number of µOps generated, minimizes register usage, and eliminates intermediate dependencies. The result is a leaner, more efficient pipeline with better decode and fetch characteristics. By collapsing multiple operations into a single instruction, we unlock micro-op fusion benefits and streamline the critical path of the GEMM kernel.
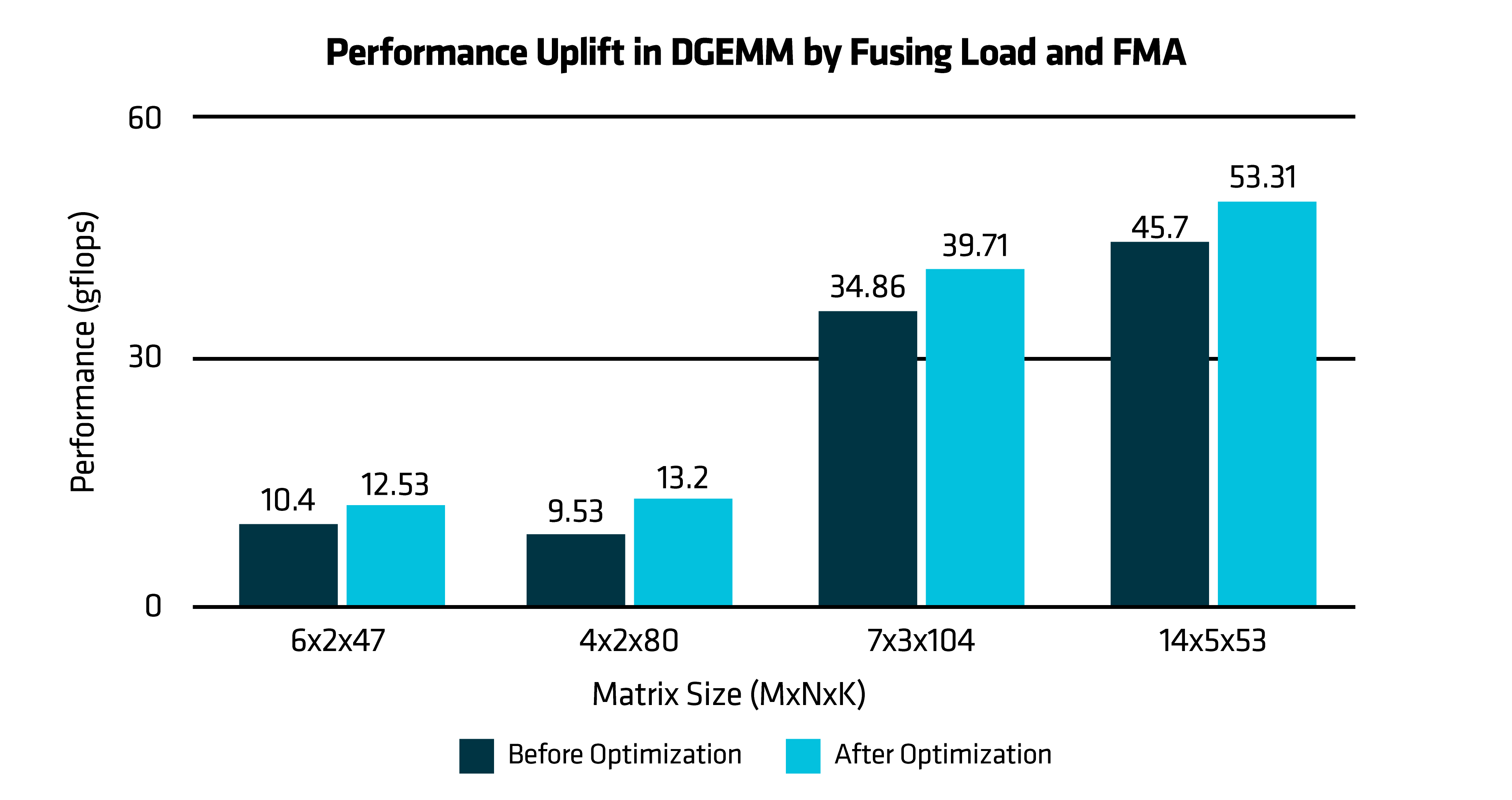
Figure 5: Performance Uplift in DGEMM by Fusing Load and FMA
The performance chart compares the baseline implementation with the optimized DGEMM kernel, demonstrating a 21% performance improvement. This gain is primarily due to the use of fused loads and FMA instructions.
Performance Gains by fusing load and FMA: The performance chart compares the baseline implementation with the optimized DGEMM kernel, demonstrating a 21% performance improvement. This gain is primarily due to the use of fused loads and FMA instructions.
Branch-Free Edge Handling with Masked Instructions
Handling edge cases—such as leftover rows or columns that don’t align with the vector width—is a common challenge in GEMM kernels. Traditionally, these tails are managed using conditional branches or scalar fallbacks. While functionally correct, this approach introduces control flow divergence, disrupts instruction prefetching, and prevents vectorization in the tail paths. Such branching patterns degrade performance by breaking the linearity of the instruction stream. They reduce instruction cache locality and prevent the CPU from leveraging SIMD execution units efficiently.
To address this, we came up with two strategies.
🔹 Strategy 1: AVX-512 Masked Ops
The first technique leverages AVX-512’s masking capabilities. By preparing a mask that represents the number of valid elements in the tail (e.g., 5 out of 8), we can perform masked loads and computations that zero out inactive lanes. This is achieved using MASK_KZ, which is a symbolic macro that typically expands to “{k2}{z}”. For example:
Mov rdx, (1 << 5) – 1 // Prepare mask: lower 5 bits set (0b00011111)
Kmovw k2, rdx // Move mask from rdx into mask register k2
vmovupd zmm1 MASK_KZ(2), [rax] // Masked load: load 5 elements from [rax] into zmm1, zero others
🔹Strategy 2: Vector Size Switching
The second technique involves switching between vector widths—ZMM (512-bit), YMM (256-bit), and XMM (128-bit)—based on the number of remaining elements. Since AVX-512 registers overlap with AVX and SSE registers, this allows us to reuse the same register names while adjusting the instruction width. For instance, if 12 elements remain, we can load 8 with a ZMM instruction and the remaining 4 with a YMM instruction, maintaining full vectorization without branching.
AVX-512 registers overlap with AVX registers.
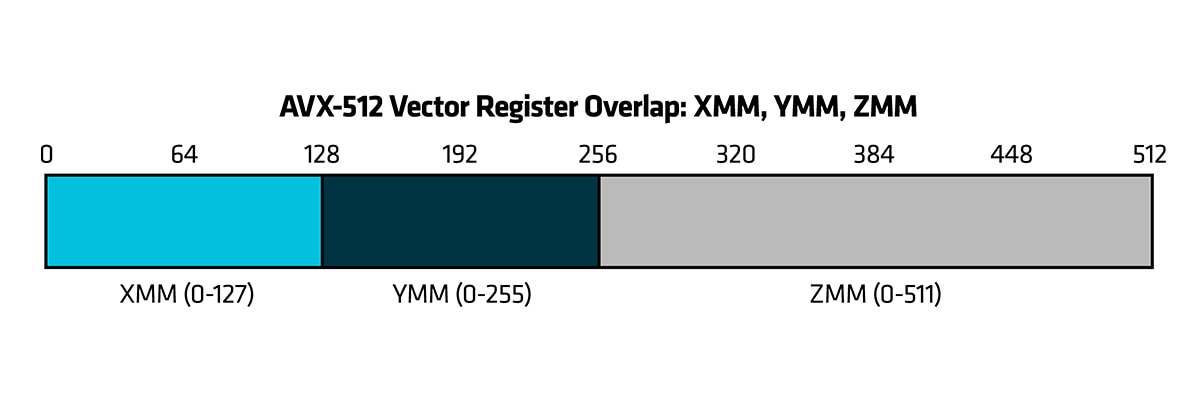
Figure 6: AVX-512 Vector Register Mapping: From XMM to ZMM
AVX-512 Vector Register Overlap: XMM, YMM, ZMM : This image illustrates the overlap among vector registers: XMM, YMM, and ZMM.
The XMM register occupies the lower 128 bits (bits 0–127) of the register.
The YMM register extends the XMM register to 256 bits (bits 0–255).
The ZMM register further extends YMM to the full 512-bit width (bits 0–511), which is available in AVX-512.
All three registers — XMM, YMM, and ZMM — refer to the same physical register, just with different vector widths.
xmm0 is the lower 128 bits of ymm0, which is the lower 256 bits of zmm0.
Similarly, ymm1 overlaps with zmm1
vmovupd zmm0, [rax] // Load 8 double-precision elements (512 bits) from memory into zmm0
vmovupd ymm1, [rax] // Load 4 double-precision elements (256 bits) from the same memory into ymm1
These strategies are particularly effective on AMD “Zen 4” and “Zen 5” architecture, where masking is hardware-accelerated, and vector width switching is efficiently handled by the decode and execution units. The result is a uniform, cache-friendly execution path that avoids scalar slowdowns and maintains SIMD throughput even in the tail regions.
The performance chart compares the baseline implementation against the optimized version of DGEMM kernel, which shows a performance improvement of 14%, which is due to branch-free handling of edge cases in GEMM kernel.
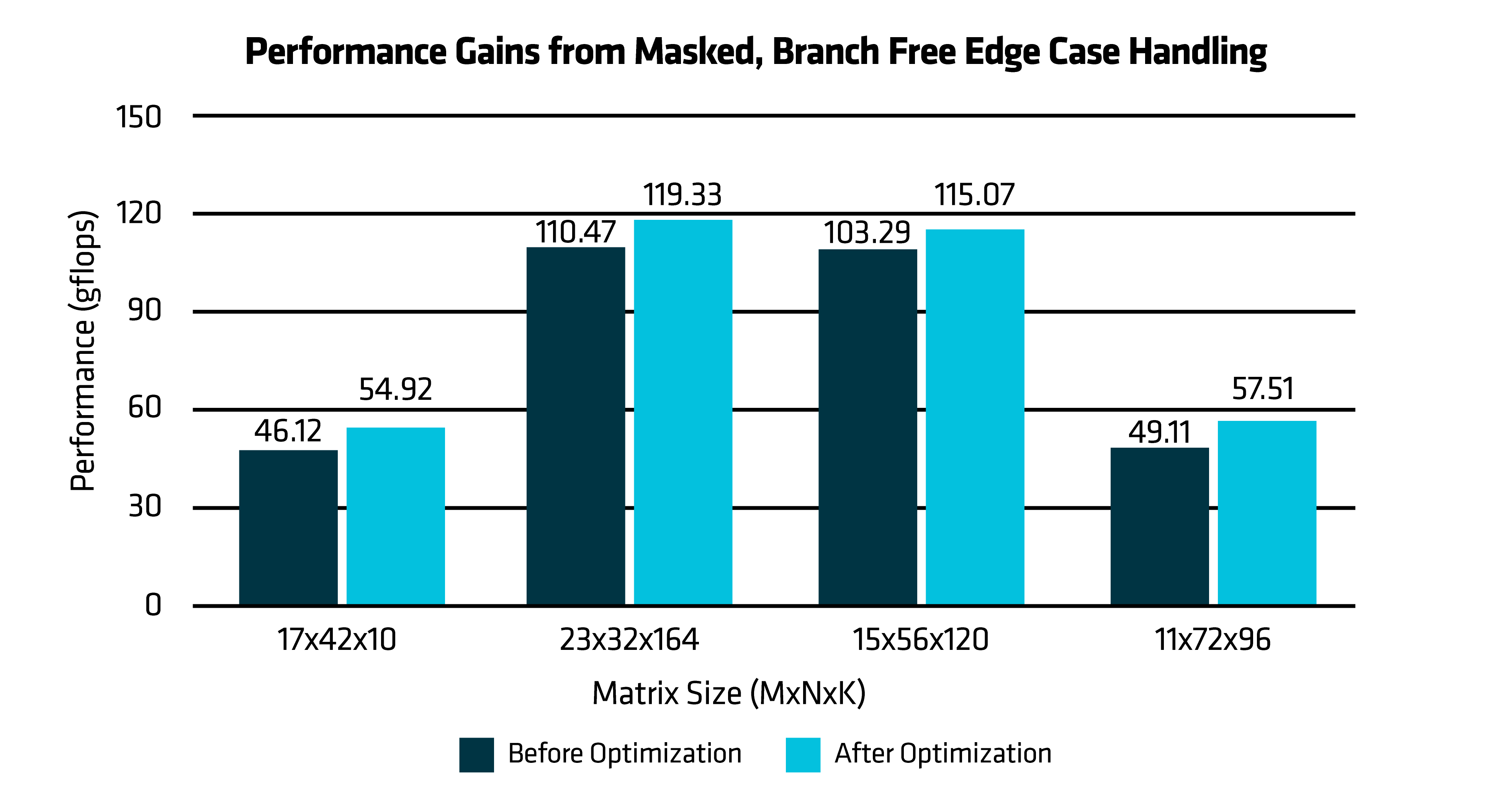
Figure: 7 Performance Gain from Masked, Branch Free Edge Case Handling
The performance chart compares the baseline implementation against the optimized version of DGEMM kernel, which shows a performance improvement of 14%, which is due to branch-free handling of edge cases in GEMM kernel.
The Payoff
These microarchitectural refinements brought dramatic improvements:
- Substantial speedups in edge-case DGEMM paths
- Reduced instruction stalls and frontend bottlenecks
- Better alignment with Zen’s fetch/decode/memory subsystems
- Smooth execution even in tail and edge conditions
The following performance graph reflects the impact of integrating all four optimization approaches into a single refined DGEMM kernel, which shows an overall performance improvement of 20% across matrices of varying sizes and shapes. This combined implementation demonstrates the full potential of architecture-aware tuning on AMD “Zen 4” and “Zen 5” architecture.
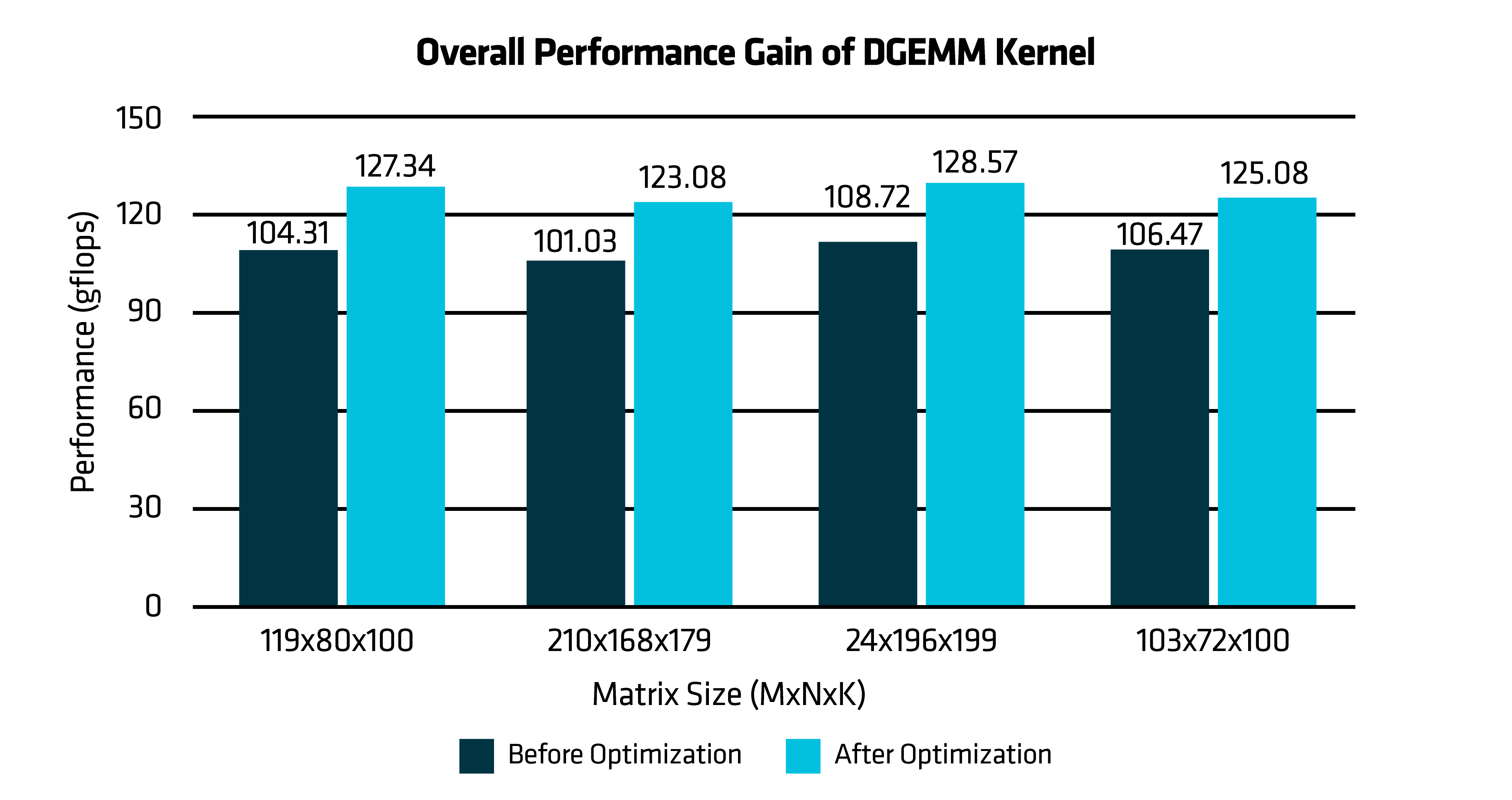
Figure 8: Overall Performance Gain of DGEMM Kernel
Final Thoughts
Great performance isn’t just about big matrices and deep pipelines — it’s about respecting the architecture and designing for the small stuff with surgical precision.
Tuning AOCL-BLAS's GEMM with Zen-aware optimizations, we’ve unlocked performance from the unlikeliest of places — tiny matrices — with massive payoff.
To explore AOCL in greater depth, including its full suite of optimized numerical libraries, visit the AMD AOCL Developer Portal. Developers interested in experimenting with AOCL-BLAS can access the source code and contribute via the AOCL-BLIS GitHub repository. Dive in and accelerate your applications with optimized performance on AMD hardware!









